Unit 8 : Additional Problems#
For those looking for additional problems outside of past exam questions and the worked problems in the lectures please consider the following in the reading list.
Unworked Problem : Thermal Neutrons#
Thermal neutrons have energies of order \( 0.025 \, \text{eV} \). If a target is irradiated by such neutrons, are the resulting reactions likely to be direct or compound-nucleus? Explain your reasoning.
Unworked Problem : Independence Hypothesis#
A study of the independence hypothesis compares the reactions \( ^{46}Ti(\alpha, pn)^{48}V \), \( ^{34}S(^{16}O, pn)^{48}V \), and \( ^{28}Si(^{22}Ne, pn)^{48}V \):
Based on compound-nucleus theory, what do you expect this study to find?
The cross section for \( ^{46}Ti(\alpha, pn)^{48}V \) peaks at an \( \alpha \)-kinetic energy of \( 32 \, \text{MeV} \) (in the lab frame). At what \( ^{16}O \) and \( ^{22}Ne \) kinetic energies would you expect the other two cross sections to peak, based on your answer to part (a)?
The magnitude of the cross section for \( ^{46}Ti(\alpha, pn)^{48}V \) is found to be much higher than for \( ^{34}S(^{16}O, pn)^{48}V \). Does this invalidate compound-nucleus theory? Explain your reasoning. (Hint: consider the charges of the nuclei involved in the reactions.)
Unworked Problem : Reaction Resonances#
The diagram shows a resonance in the reaction \( ^{13}C(n, \gamma)^{14}C \):
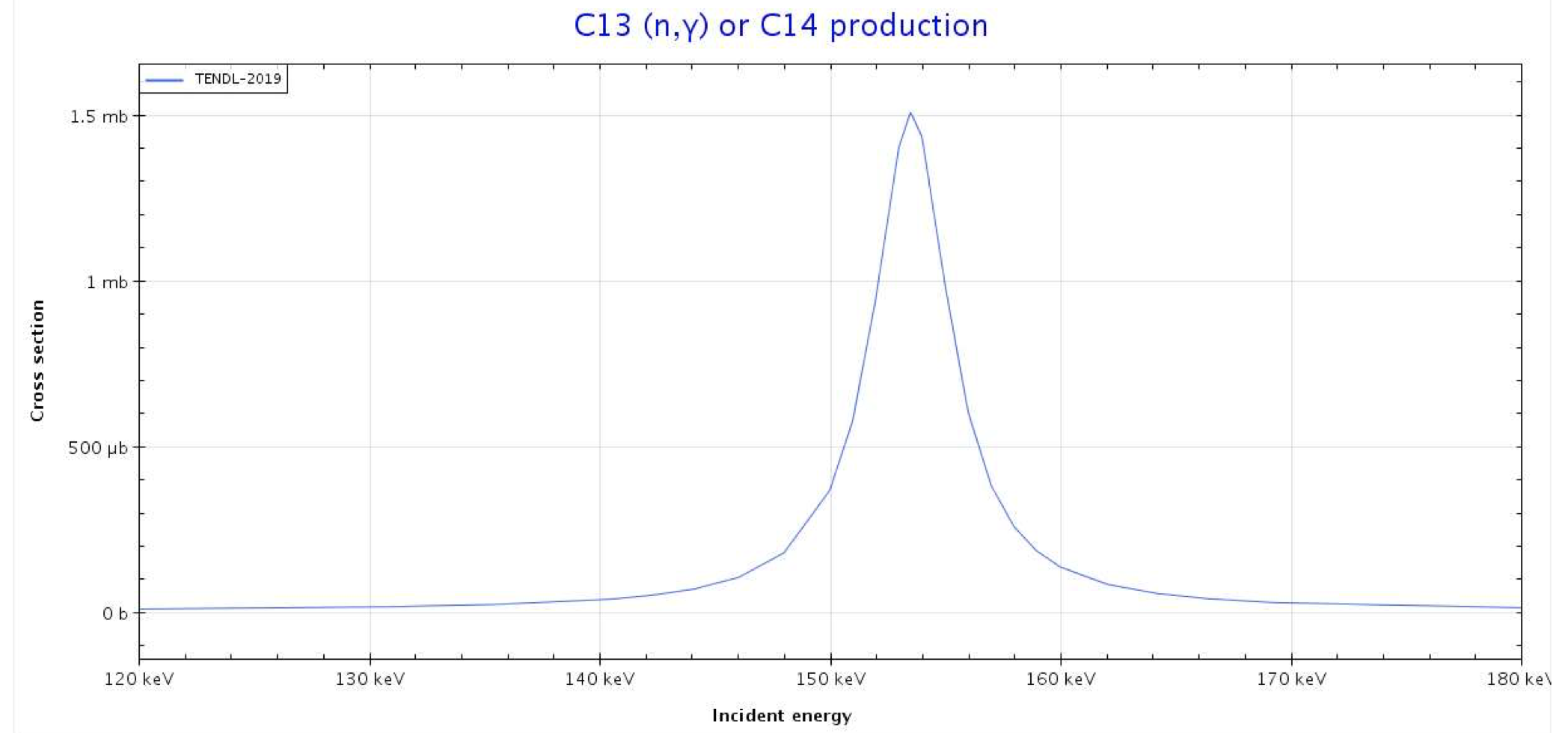
Calculate the momentum of the neutron at the peak of the resonance. (Hint: recall that a neutron with a kinetic energy of order \( 150 \, \text{keV} \) is not relativistic.)
Hence calculate the kinetic energy of the \( ^{14}C \) nucleus after the collision (but before the \( \gamma \)-emission).
Determine the energy of the excited state corresponding to this resonance. Compare your answer with the known energy levels of \( ^{14}C \) (see, for example, the Triangle Universities Nuclear Laboratory website).
Estimate the lifetime of this state.
Relevant atomic masses:
\( ^{13}C: 13.0033548 \, u \)
\( ^{14}C: 14.0032420 \, u \)
\( n: 1.0086650 \, u \)
\( 1 \, u = 931.502 \, \text{MeV/c}^2 \)
Unworked Problem : Momentum Transfer#
A \( (d, p) \) scattering experiment on a \( ^{40}Ca \) target (i.e. \( ^{40}Ca(d, p)^{41}Ca \)) finds a peak in the proton energy spectrum at a proton energy of \( 10.29 \, \text{MeV} \), measured at an angle of \( 67.5^\circ \) (in the lab frame) to the initial deuteron direction. The energy of the deuteron beam is \( 7.00 \, \text{MeV} \):
Find the momenta of the incident deuteron and outgoing proton.
Show that, assuming that the target \( ^{40}Ca \) atom is stationary, the momentum of the \( ^{41}Ca \) atom is given by:
\[ p_{Ca}^2 = p_d^2 + p_p^2 - 2 p_d p_p \cos \theta \]where \( \theta \) is the angle between the incoming deuteron and outgoing proton directions, i.e., \( 67.5^\circ \). Hence calculate the momentum and kinetic energy of the \( ^{41}Ca \) atom. (Hint: draw the triangle corresponding to the conservation of momentum, \( \vec{p}_d = \vec{p}_p + \vec{p}_{Ca} \). Recall that all the particles in this reaction are non-relativistic.)
Calculate the Q-value of the reaction \( ^{40}Ca(d, p)^{41}Ca \).
Using your answers to parts (b) and (c), calculate the energy of the excited state of \( ^{41}Ca \) that produces this peak in the proton energy spectrum.
Relevant atomic or particle masses:
\( ^{40}Ca: 39.9625909 \, u \)
\( ^{41}Ca: 40.9622779 \, u \)
Deuteron: \( 2.0135532 \, u \)
Proton: \( 1.0072765 \, u \)
