10. Complex Numbers

The material in this topic is also covered in chapter 6 of the textbook Martin and Shaw “Mathematics for Physicists”. In Boas “Mathematical Methods in the Physical Sciences” it is in chapter 2.

10.1. Introduction

Complex numbers are used in many areas of physics. You will soon meet them in waves and oscillations, electromagnetism, and quantum mechanics. This section of the course is designed to help you develop the skills to tackle mathematical problems involving complex numbers across your university course.

10.2. Definition

A complex number is a number that has real and imaginary parts, it is the sum of a real number and an imaginary number. An imaginary number is one that is proportional to \(i\) where \(i^2=-1\) i.e. \(i=\sqrt{-1}\). The definition of a complex number, \(z\) is

\[z=x+iy\]

where \(x\) and \(y\) are real numbers and \(i^2=-1\). We call \(x\) the real part, \(\mathrm{Re}(z)\), and \(y\) the imaginary part, \(\mathrm{Im}(z)\). Two complex numbers \(z_1\) and \(z_2\) are only equal if both their real parts and their imaginary parts are equal. i.e. \(z_1=z_2\) if and only if \(\mathrm{Re}(z_1)=\mathrm{Re}(z_2)\) and \(\mathrm{Im}(z_1)=\mathrm{Im}(z_2)\).

10.3. Addition and subtraction

To add complex numbers together, you need to separately add their real and imaginary parts i.e. if \(z_1=x_1+iy_1\) and \(z_2=x_2+iy_2\) then

\[z_1+z_2=(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+(y_1+y_2)i.\]

Similarly for subtraction we obtain;

\[z_1-z_2=(x_1+iy_1)-(x_2+iy_2)=(x_1-x_2)+(y_1-y_2)i.\]

10.4. Multiplication

To multiply a complex number by a real number we must multiply both the real and imaginary parts of the complex number. For example, let us multiply the complex number \(z\) by a real number \(a\);

\[az=a(x+iy)=ax+iay.\]

We can also multiply a complex number by an imaginary number. For example, let us multiply the complex number \(z\) by an imaginary number \(bi\);

\[zbi=(x+iy)bi=bxi+byi^2=bxi-by=-by+bxi.\]

To multiply two complex numbers we perform the multiplication in the same way as we would multiply out brackets in normal algebra i.e.

\[\begin{split}\begin{aligned} z_1z_2=&(x_1+iy_1)(x_2+iy_2)\\ =&x_1x_2+x_1y_2i+y_1x_2i +y_1y_2i^2\\ =&x_1x_2+x_1y_2i+y_1x_2i -y_1y_2\\ =&(x_1x_2-y_1y_2)+(x_1y_2+y_1x_2)i\\ \end{aligned}\end{split}\]

10.5. Argand Diagram

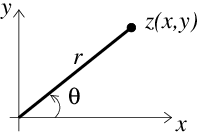
Fig. 10.1 An Argand diagram depicting a complex number, z = x + iy with the x axis representing the real part of z and the y axis representing the imaginary part of z. The complex number z is the point marked on the graph with a filled black circle. The line from the origin to the point z is shown as a thick black line with distance labelled as r. The angle between the x-axis and the line from the origin to the point z is labelled as θ. These labels (r, θ) correspond to polar coordinates.

An Argand diagram, shown in figure Fig. 10.1, is a graphical way of representating complex numbers. The real components are represented on the horizontal axis and the imaginary components on the vertical axis. We call this space the complex plane.

Using the complex plane we can visualise the geometrical interpretation of adding two complex numbers (see Fig. 10.2).

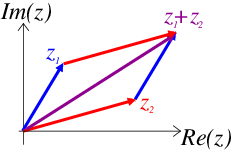
Fig. 10.2 An Argand diagram showing addition of two complex numbers z₁ and z₂.

The sum of two complex numbers \(z_1\) and \(z_2\) depicted as points on the complex plane in an Argand diagram is the point obtained by forming a parallelogram in which the sides are the lines from the origin to the points \(z_1\) and \(z_2\). If you consider these lines as vectors you can see that the addition of complex numbers on the complex plane is the same as adding vectors on a graph.

10.6. Polar form

The polar form of a complex number is another way that we can represent a complex number. It has two parts: the modulus and the argument. The modulus of \(z\) is the absolute value or magnitude, written as \(|z|\). On the Argand diagram (Fig. 10.1) the modulus of the complex number \(|z|\) is the distance, \(r\), of the point \(z\) from the origin. By Pythagoras’ theorem we can calculate this as;

\[ |z|=r=\sqrt{x^2+y^2}. \]

The argument (or phase) of \(z\) is the angle, \(\theta\), between \(r\) and the positive \(x\)-axis. Here the standard convention is used whereby angles are measured anticlockwise from the positive \(x\)-axis. The argument of \(z\) is often written as \(\mathrm{arg}(z)\). We can calculate the angle using trigonometry as;

\[ \mathrm{arg}(z)=\theta=\tan^{-1}{\left(\frac{y}{x}\right)} \]

Usually we use the principal argument which is defined as the angle in the range \(-\pi<\theta\le\pi\). We can also write \(\theta\) in terms of the modulus, \(r\), i.e.

\[ \tan{\theta}=\frac{y}{x},\quad\quad \sin{\theta}=\frac{y}{r}\quad{\text{and}}\quad\cos{\theta}=\frac{x}{r}. \]

Therefore we can write any complex number \(z\) in the trigonometric form or polar form which is equivalent to expressing \(z\) in polar coordinates i.e.

(10.1)\[z=r(\cos{\theta}+i\,\sin{\theta}).\]

Using Euler’s formula, \(e^{i\theta}=\cos{\theta}+i\,\sin{\theta}\), a complex number can be written in exponential form as

(10.2)\[ z=re^{i\theta}. \]

Let us consider a famous example of a complex number in this form. Let \(r=1\) and \(\theta=\pi\) then using equations (10.1) and (10.2) we have

\[ e^{i\pi}=\cos{\pi}+i\,\sin{\pi}=-1. \]

This particular example appears in the equation known as Euler’s identity:

\[ e^{i\pi}+1=0 \]

Complex numbers are used in most areas of physics and the exponential form is particularly powerful.

10.7. Complex conjugate

Every complex number has associated with it another complex number which is known as its complex conjugate. The complex conjugate of a complex number \(z=x+iy\) is given by;

\[ \bar{z}=z^{*}=x-iy=r(\cos{\theta}-i\sin{\theta})=re^{-i\theta}. \]

Both notations \(\bar{z}\), “z bar”, or \(z^{*}\), “z star”, are used to mean the complex conjugate of \(z\).

On an Argand diagram the complex conjugate is the reflection in the real axis (the \(x\)-axis) as shown in figure Fig. 10.3.

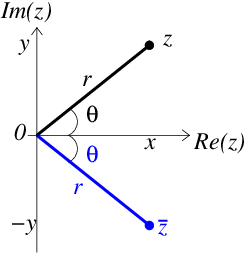
Fig. 10.3 An Argand diagram showing the complex number z (black filled circle) and its complex conjugate z̄ (blue filled circle).

Multiplying a complex number by its complex conjugate gives the square of its modulus:

\[ z^{*}z=z\bar{z}=(x+iy)(x-iy)=x^2+y^2=r^2=|z|^2. \]

Note that multiplying a complex number by its complex conjugate gives a real number.

We can write the real and imaginary parts of a complex number in terms of its complex conjugate as;

\[ \mathrm{Re}(z)=\frac{z+\bar{z}}{2}\quad{\text{and}}\quad\mathrm{Im}(z)=\frac{z-\bar{z}}{2i} \]

This shows that a complex number is real if and only if it equals its own conjugate i.e. if \(z=\bar{z}\) then \(z\) is real since its imaginary part is zero.

10.8. Division

Division of a complex number \(z_1\) by another complex number \(z_2\) is complex. It is not directly possible to divide one complex number by another, so we have to use a mathematical trick to enable this. There are three ways you can approach division of a complex number \(z_1\) by another complex number \(z_2\):

1. Using the complex conjugate:

\[ \frac{z_1}{z_2}=\frac{z_1z_2^{*}}{z_2z_2^{*}}=z_1\frac{z_2^{*}}{|z_2|^2}=\frac{(x_1+iy_1)(x_2-iy_2)}{x_2^2+y_2^2}=\frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+\frac{(y_1x_2-x_1y_2)i}{x_2^2+y_2^2} \]

2. Using the complex exponential approach:

\[ \frac{z_1}{z_2}=\frac{r_1e^{i\theta_1}}{r_2e^{i\theta_2}}=\frac{r_1}{r_2}e^{i\theta_1}e^{-i\theta_2}=\frac{r_1}{r_2}e^{i(\theta_1-\theta_2)} \]

3. Using the polar form using the following trigonometric identities :

\[\begin{split} \begin{aligned} \sin{(a\pm b)}=&\sin{a}\cos{b}\pm\cos{a}\sin{b}\\ \cos{(a\pm b)}=&\cos{a}\cos{b}\mp\sin{a}\sin{b}. \end{aligned} \end{split}\]

Note that these trigonometric identities will be given to you in an exam on the formula sheet so you don’t need to worry about memorising them. Division can be done as

\[ \frac{z_1}{z_2}=\frac{r_1}{r_2}(\cos{(\theta_1-\theta_2)}+i\sin{(\theta_1-\theta_2)}) \]

by simply dividing the absolute values and subtracting the arguments.

10.9. Powers and de Moivre’s theorem

Taking a complex number to the power \(n\) where \(n\) is an integer can be done most easily by considering the exponential form of a complex number, given in equation (10.2). Taking the exponential form to the power \(n\) gives

\[ z^n=(re^{i\theta})^n=r^ne^{i n\theta}. \]

Putting this into trigonometric form gives

\[ (r(\cos{\theta} + i\sin{\theta}))^n=r^n(\cos{n\theta}+i\sin{n\theta}). \]

This reveals another trigonometric identity, known as de Moivre’s theorem, also called de Moivre’s formula or de Moivre’s identity. It states that

(10.3)\[ (\cos{\theta} + i\sin{\theta})^n=\cos{n\theta}+i\sin{n\theta} \]

for any integer \(n\).

Using de Moivre’s identity in equation (10.3) we can find, for example, that

\[ z^n+\frac{1}{z^n}=2\cos{n\theta}\quad\text{and}\quad z^n-\frac{1}{z^n}=2i\sin{n\theta} \]