4. Minima, maxima and points of inflection

4.1. Higher order derivatives

So far, we have determined the rate of change of a function. This new derivative function can be analysed for its rate of change i.e. the 2\(^{\mathrm{nd}}\) derivative. This process can be repeated as long as the derivatives are differentiable functions. These higher derivatives are very useful in analysing the original function such as determining:

• local maxima and minima

• points of inflection

• power series approximation (see next topic)

Higher order derivatives also play a role in many theoretical descriptions of the physical world. Two examples include the equation describing heat diffusion and the wave equation.

4.2. Critical points

The first derivative of a function evaluated at a point provides a measure of the instantaneous rate of change of the function at that point. When the first derivative is equal to zero, we have what is called a stationary point. Although this term is used to describe functions that vary with any independent variable, its meaning is clearest if we consider the derivative of distance with respect to time; i.e., speed. When this derivative is zero the speed is zero, and something with zero speed is stationary. Some stationary points are local maxima or minima, while others are horizontal points of inflection. You may also see these referred to as critical points. The typical analytical process to locate these points is to:

1. First determine where there are any stationary points i.e. determine were \(f'=0\)

2. Then check the sign of the second derivative \(f''\) at this point if:

   1. \(f''(x)<0\) the function is a local maxima at this point.

   2. \(f''(x)>0\) the function is a local minima at this point.

   3. \(f''(x)=0\) the function might be a local maxima, a local minima or a horizontal point of inflection. If \(f'\) has the same sign immediately above and below \(x\), then the point is a point of inflection. If it changes sign, then it is a point of minimum or a maximum.

A point for which \(f'\ne0\) whilst \(f''(x)=0\) is a point of inflection.

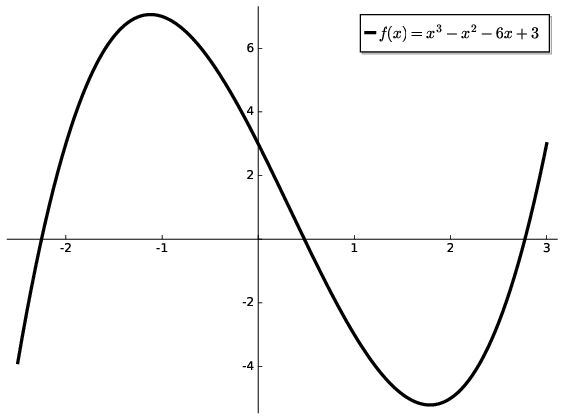
Fig. 4.1 Visualising the function \(f(x)=x^{3}-x^{2}-6x+3\) we can see that there is an obvious maximum and minimum. The change in concavity of the curve is also apparent indicating an inflection point between 0 and 1;

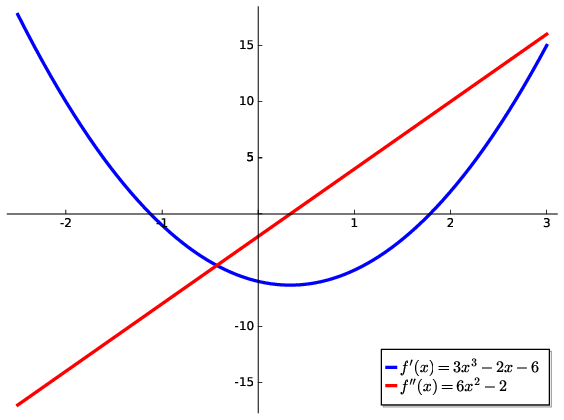
Fig. 4.2 These critical points can be determined analytically via the higher derivatives of \(f(x)\). Here the first derivative goes to zero at the max/min points and the second derivative changes sign at the inflection point.

For example, let’s evaluate the critical points of the function

\[f(x)=x^{3}-x^{2}-6x+3\]

First, evaluate where \(f'(x)=0\):

\[f'(x)=3x^{2}-2x-6\]

and determine where this is zero:

\[\begin{split}\begin{aligned} 3x^{2}-2x-6= & 0\\ x_{0}= & \frac{-2\pm\sqrt{2^{2}-72}}{6}\\ x_{0}= & -1.12,\,1.79\end{aligned}\end{split}\]

The solution to the quadratic equation indicates multiple stationary point. Next, evaluate the second derivative \(f''(x_{0})\) at these points:

\[\begin{split}\begin{aligned} f''(x) & =6x-2\\ f''(-1.12)= & -6.72\\ f''(1.79)= & 10.74\end{aligned}\end{split}\]

therefore we have a local maxima at -1.12 and a local minima at 1.79. Finally, we can check for points of inflection:

\[\begin{split}\begin{aligned} f''(x) & =6x-2=0\\ x= & \frac{2}{6}\\ x= & \frac{1}{3}\end{aligned}\end{split}\]

The original function and its derivatives are shown in Fig. 4.1 and Fig. 4.2. Indeed, even with just the minima, maxima and \(x_{0}\) values we can typically sketch most functions.

4.2.1. Absolute minima

Often in physics we encounter problems where there are more than minima in the function. Of these points, the one which has the lowest value of the function is known as the absolute minimum or the global minimum. The other minima are referred to as local minima. Finding a global minimum can be a challenging mathematical task!